Е. В. Гусева

Пензенский государственный педагогический университет им. В. Г. Белинского,

кафедра теории и методики обучения математике и информатике

e-mail: kika_zeml@mail.ru

ОБЕСПЕЧЕНИЕ ПРОПЕДЕВТИКО-ПРОФЕССИОНАЛЬНОЙ НАПРАВЛЕННОСТИ ОБУЧЕНИЯ КАДЕТОВ НА ОСНОВЕ РЕАЛИЗАЦИИ МЕЖПРЕДМЕТНЫХ СВЯЗЕЙ КУРСОВ МАТЕМАТИКИ И ИНФОРМАТИКИ

Пропеде́втика – введение в какую-либо науку, предварительный вводный курс, систематически изложенный в сжатой и элементарной форме

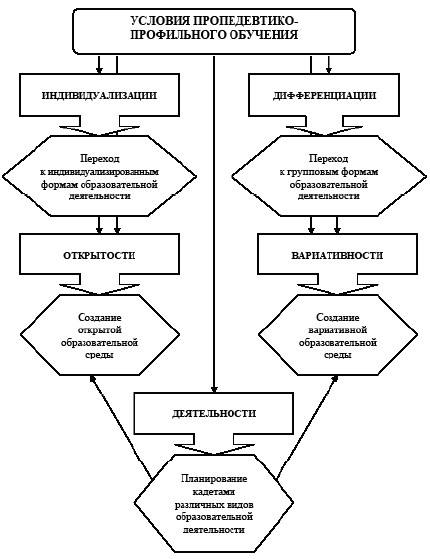
Выделим ряд основных принципов, конкретизирующих возможности работы по реализации профильного обучения в кадетских школах:

- принцип пропедевтико-профессиональной направленности;

- принцип преемственности;

- принцип деятельности;

- принцип дифференциации и индивидуализации.

Центральное место среди них занимает принцип профессиональной направленности, который изначально предполагает необходимость установления тесной связи обучения с будущей  профессиональной деятельностью (в нашем случае обучения кадетов с целью их подготовки к обучению военно-инженерным специальностям). Данный принцип предопределяет характер логического соподчинения всех остальных принципов, образующих в совокупности иерархию отраженную на следующей схеме (рис. 1).

Рис. 1. Иерархия принципов профильного обучения

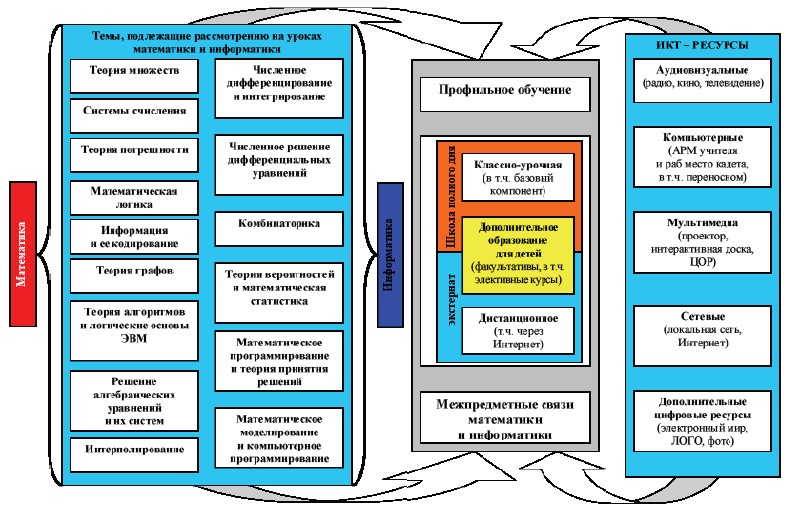
Проблема обеспечения пропедевтико-профессиональной направленности обучения и воспитания

кадетов включает как формирование их социальной и психологической готовности к реализации будущей учебно-профессиональной деятельности в соответствии с личными интересами и общественными потребностями, так и актуализацию междисциплинарных связей в организации и содержании общеобразовательной подготовки [4].

Реализация принципа пропедевтико-профессиональной направленности применительно к информационно-дидактической подготовке кадета включает в себя формирование профессионально значимых приемов использования программных продуктов в образовательном процессе; обеспечение соответствующего аппарата для изучения общеобразовательных дисциплин с пропедевтико-профессиональным наполнением; предварительную методологическую подготовку к непрерывному самообразованию в области профессионально-значимых приложений обучения на основе целесообразного использования современных программных средств. Перечисленные задачи требуют системного решения как на содержательном (отбор и построение содержания соответствующих элективных курсов, обеспечивающих пропедевтико-профессиональную подготовку кадета), так и на  деятельностно-процессуальном уровнях организации процесса обучения с учетом специфики избранного военно-инженерного профиля.

Любая педагогическая система определяется как объединение взаимосвязанных структурных и функциональных компонентов, которое остается устойчивым при изменениях и подчиненное целям воспитания и образования. Дидактической системе присущи следующие основные признаки:

- целостность;

- взаимосвязанность элементов;

- связь со средой.

Целостность системы означает общую цель, достижению которой служат части системы. Взаимодействие и взаимопроникновение частей системы, невозможность их разрыва является необходимым условием существования системы. Взаимосвязанность элементов системы заключается в том, что изменение одного параметра системы оказывает влияние на все остальные. Связь системы со средой выражается в том, что система является составной частью среды, ее элементом, состоящим, в свою очередь, из элементов более низкого порядка [5].

Согласно А. В. Могилеву модель методической системы обучения, наиболее адекватно отражающая изменения в ходе информатизации и компьютеризации образования, должна соответствовать следующим принципам:

- предметность;

- локальность;

- динамичность.

Приведенная выше схема соответствует реализации вышеперечисленных принципов и позволяет, не отрицая традиционных подходов к проектированию и реализации учебного процесса, наметить пути развития методической системы обучения в условиях применения ИКТ при обучении темам  рассматриваемых как в математике, так и в информатике.

Как известно, межпредметные связи между математикой и информатикой носят двусторонний характер: изучение математики должно подготавливать изучение информатики (логическая и алгоритмическая подготовка, приближенные вычисления и т. д.); в свою очередь, курс информатики имеет выходы в математику. Выделим следующие вопросы, связанные с возможностями использования знаний по информатике в курсе математики:

- какие темы курса математики должны быть наиболее тесно связаны с курсом информатики;

- какие изменения в содержании этих тем и методике их изучения произойдут при увязке их с курсом информатики;

- какие задачи и в каком количестве следует доводить до составления программы решения с помощью компьютера;

- сколько часов в течение учебного года, отведенных на изучение математики, может быть проведено в компьютерном классе;

- какова может быть методика компьютерного решения задач курса математики.

Решение этих вопросов лежит в основе реализации двусторонних связей математики и информатики как в рамках базовых, так и элективных курсов.

Покажем на схеме (рис.2) процесс реализации межпредметных связей математики и информатики на примере профильного обучения в кадетских классах.

Рис. 2. Схема процесса реализации межпредметных связей математики и информатики в кадетских классах

Приведенная схема включает в себя темы, подлежащие рассмотрению как в рамках математики, так и в рамках изучения информатики. Эти темы целесообразно рассматривать как дидактические единицы межпредметных элективных курсов, которые являются неотъемлемой составляющей профильного обучения. Разработка данных курсов станет предметом нашего дальнейшего исследования.

Список литературы

1. Бедерханова В.П., Бондарев П.Б. Педагогическое проектирование в инновационной деятельности. Краснодар, 2000.

2. Беспалько В.П. и др. Системно-методическое обеспечение учебно-воспитательного процесса подготовки специалиста. М.: Высшая школа, 1989.

3. Джонс Дж., Методы проектирования. М.: Мир, 1986.

4. Михеев В.И., Моделирование и методы теории измерений в педагогике. М.: Высш. школа, 1987.

5. Монахов В.М. Педагогическое проектирование – современный инструментарий дидактических исследований // Шк.технологии. 2001. № 5. С. 75–89.

***

Известия Пензенского государственного педагогического университета имени В. Г. Белинского

«Общественные науки» № 24 2011 УДК 372.851